Discourse in the Japanese vs. American math classroom
Guest Contributor: Daniel Lee
I was in my colleague’s world history classroom, and I was flabbergasted. “Look at the damage you did to our nation, Germany! You’ll pay for this!” It was one of my more timid students, howling his indictment across the room.
I teach 9th grade math, and I perceive many of my students as being on the quieter side. They can be reluctant to speak up, and less than eager to volunteer to answer my questions. Which is why it was so shocking when I witnessed students from my classes participating so vigorously in this simulation on World War I.
“I don’t even know how to respond,” was Germany’s sober reply. “I agree we deserve these sanctions.” Another student I thought of as shy.
The voices shot through the room that day. Some students maybe even took the simulation a little too seriously. (Actual tears were shed.) I couldn’t help but sit back in awe of these beautiful conversations. I had never seen my students so passionate about their coursework, and I recognized through their conversations that they had truly mastered knowledge about World War I.
I couldn’t help but wonder: Was this possible in math?? Could I develop, in my math classes, this same level of passionate discourse?
If so, I knew there needed to be a radical shift in my lesson structure to increase and amplify student voice. At the time, I had been reading about James Stigler’s research on Japanese and American math teachers, and I thought I might find the answer if I followed in the footsteps of the more successful Japanese model…
The Japanese Classroom vs. the American Classroom
In his book Helping Children Succeed, Paul Tough describes an international research project conducted by James Stigler on math teachers in the United States and Japan. Stigler found a stark difference in the general structure of instruction for classes in each country.
In Japan, teachers introduce a new mathematical concept by presenting an unfamiliar problem to students to grapple with on their own. Most of the students answer the new problem incorrectly, but the teacher guides the discussion to generate conversation about students’ mathematical thinking. Eventually, the teacher guides students in their thinking to uncover a solution, which is ultimately proposed by students, rather than the teacher.
In contrast, the American classroom begins with the teacher sharing a method of solving a certain problem with the expectation that students copy the solution, memorize it, and use it for subsequent problems the teacher assigns. Students practice these problems over and over again to internalize them, with the hope that success is maximized through repetition of error-free work. While the American classroom eliminates the frustration of not knowing what to do, it removes the possibility of building an intellectual capacity for solving problems you are unfamiliar with. As math educators we have to ask ourselves what skill are we teaching: the ability to follow steps or the ability to build logic and solve problems?
When reflecting on this in relation to my classroom, I realized I more often than not followed the script of the American classroom. And, unfortunately, a byproduct of the American classroom structure is the immediate focus on correct answers, which shuts out opportunities for students to converse about their thought process and misconceptions they might have. What I needed was a way to transition to the Japanese model to generate more discourse.
The 5 Practices
The most powerful framework I’ve found for replicating the Japanese classroom is the 5 Practices for Orchestrating Productive Mathematical Discussions. This framework that Margaret Smith and Mary Kay Stein developed breaks down the launch and synthesis of any math activity into five components:
Anticipating — What are the likely student responses to challenging math activities and what questions should we ask students who provide those responses?
Monitoring — What are students’ actual responses?
Selecting — Which students should share their work during whole-group discussion?
Sequencing — What order should they share those responses?
Connecting — How do you build connections between responses to capitalize on key mathematical ideas?
Whenever I re-read the 5 Practices I am reminded of the strengths of the framework:
It opens a consistent lesson planning pathway for students to be in their zone of proximal development (ZPD).
It celebrates every strategy students may use to approach a problem.
If implemented with fidelity, students are driving solutions, rather than the teacher. (Sound familiar?)
For teachers who are used to following the American regimen for lessons, the 5 Practices framework can transform the lesson planning process. To anticipate, teachers must develop expectations for how students might interpret a problem. When empathizing with the student, are we biasing one approach to solving a problem? Or are we truly allowing different modalities of thought to thrive? By carrying a bias for one means of expressing a solution, we eliminate all opportunities for students who see the problem differently to participate in the discussion of the classroom.
But theorizing wasn’t enough to convince me. I still had a fear that students wouldn’t be able to learn if I didn’t feed them the steps for how to do so. So, I decided to observe a veteran teacher who utilizes the 5 Practices and collect data on student voice in his classroom as compared to mine.
Veteran vs. Rookie
I wanted to benchmark the data from this veteran teacher against my own to see if there were any significant differences. So we used the TeachFX app to measure concretely the proportion and patterns of student talk time versus teacher talk time in each of our classrooms. I was astounded by the results.
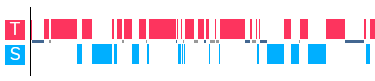
Veteran teacher’s metrics from TeachFX analysis
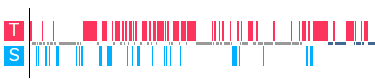
My TeachFX metrics from a lesson early in my first year teaching
While we had similar statistics for total teacher talk time, the veteran teacher doubled the level of student talk in his classroom compared to mine. What I noticed when looking at the visual breakdown of our data was that he did this through the questions he had developed to connect student responses. A reciprocity between teacher and student talk emerged. Looking at my own data, I saw periodic stretches of strictly teacher talk with no room for students to share responses. And further, when listening back to the recording from the veteran teacher’s classroom, he never gave an answer to a math question he asked his students. He wanted them to develop their own solutions and explain their reasoning.
The veteran teacher’s TeachFX report shows a reciprocity between teacher and student talk and students used mathematical reasoning to talk through the problem he posed.
Even though I asked more questions, my TeachFX report had less student talk and shorter contributions from students because I asked students to provide answers rather than explain their thinking.
The veteran teacher’s classroom reminded me of the Japanese model and provided me an exemplar for how discourse should be developed in the math classroom. There is too much lost if I continue to follow my old habits. Problem solving is an essential skill in an ever-changing economy, and the math classroom is where we can develop the foundations of that skill.
I’m not sure I’ll ever have students yelling passionately about systems of equations the way my colleague had our students debating the consequences of World War I. But I do know that my students aren’t really as shy to participate as I first thought, and that following the 5 Practices is sure to improve the level of discourse in my classroom.